超声波角测法中测距取值的研究
作者:钧测检测 发布日期: 浏览次数:
摘要:提出了“同声时等效测距法”的理念,研究采用阶梯形匀质试件上已知超声波对测声时的测距作为角测法直角三角形的斜边,根据勾股定理,反推可得到角测法构件边缘至换能器直径内某点的直角边距。试验结果表明采用“同声时等效测距法”确定的测距接近角测法的真实测距,比现行CECS标准规定的方法可靠、可行。
关键词:超声波;角测法;同声时等效法;测距
CECS 02 《超声回弹综合法检测混凝土强度技术规程》(以下简称CECS 02标准)从1985年颁布到2005年修订已经使用了33年,按理论分析,它是一种优于回弹单一法无损检测混凝土现场强度的有效技术,但在建设工程领域一直未得到广泛的应用和大家的认可。随着我国工程技术不断更新和发展,回弹法检测技术中“碳化”问题的瓶颈困扰不能解决[1], CECS 02标准为适应工程建设需要,也急需对相关内容进行不断完善,期望新修定的标准通过提高检测精度、简化现场操作方法等技术手段,使超声回弹综合法成为无损检测现场混凝土强度的首选技术。
一、 问题的提出
1.1 现行标准中的角测方法
在超声波检测方形构件的工程中,时有被测构件旁边存在墙体、管道等障碍物,只有两个相邻表面可供检测,即无法将2个换能器布置成对测法检测,此时仍然可以进行综合法测强,即在两个相邻表面的对应位置布置超声测点,采用丁角方法测量混凝土声速。CECS 02 《超声回弹综合法检测混凝土强度技术规程》(以下简称CECS 02标准)附录B.1超声波角测方法中关于角测方法的规定如下:当结构或构件被测部位只有两个相邻表面可供检测时,可采用角测方法测量混凝土中声速。每个测区布置3个测点,换能器布置如图1所示。
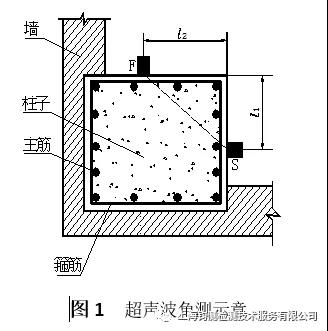
CECS 02标准同时又规定:为使超声波能充分反映构件内部混凝土的质量,同时还要尽可能避开钢筋的影响,布置超声测点时最好使换能器尽量离开构件边缘远一些,布置超声角测点时,换能器中心与构件边缘的距离、不宜小于200mm。在检测中可能会遇到一个表面较窄另一表面较宽的构件,所以布置测点时不要求与相等,但二者相差不宜大于2倍。
角测时超声测距应按下列公式计算:

1.2 平测法中的修正距离
当超声波采用平测方法检测时,我国早在上世纪80年代已有定论:真实测距即不是两个换能器的内边缘间距,也不是两个换能器的中到中间距。
平测法中超声波实际传播距离介于换能器的中~中与边~边二者距离之间,比两个换能器的中到中间距短、内边缘间距长。即在超声波平测法时超声测距中存在一个与换能器直径Ф相关的修正距离a(0 < a < Ф)。在平测法检测时,如果测距不作修正,则取中~中时,计算的声速值偏大;边~边时,计算的声速值偏小。假设每一对发射、接收换能器,修正距离a是一个小于换能器直径的定值,且测距越小、误差越大[2]。
1.3 对现行角测方法的质疑
众所周知,在超声波对测方法中,测距非常明确,是2个换能器平行辐射面间相隔的距离。在超声波平测方法中,真实的测距是2个换能器内边缘间距加修正距a。
在超声波角测方法中,其测距采用三角形的直角边(换能器与构件边缘的距离)通过勾股定理计算得出。由图1(CECS 02标准中的图B.1.1)超声波角测示意图显而易见,超声波角测时,布置在直角边上的一对换能器的测距,可以视作为两换能器与构件边缘的距离构成的直角三角形的斜边。其问题是斜边距取两个换能器的中心点距,还是两个换能器的近边缘距(两换能器间最短直线点距)显然,斜边距取近边缘距比中心点距小;取远边缘距比中心点距大。
设换能器在构件直角边上对称布置,换能器的直径为38mm,取近边缘距200mm~500mm时,其与中心点距的测距比值见表1。由表1可知,当近边缘距为200mm时,测距的比值最大,即检测误差大;随近边缘距的增大,其测距的比值逐渐降低;400mm以上时,两者的比值在10%以内。

在CECS 02标准中关于附录B.1超声波角测方法的编制说明,有如下一个叙述:“大量对比试验表明,可采用F、S换能器中心点与构件边缘的距离、 ,按几何学原理计算超声测距;用此测距与角测的声时值计算所得的声速值,与对测的声速值没有明显差异,不需作任何修正。”作者对此叙述存疑,并就CECS 02标准的附录B.1——关于超声波角测方法的正确性进行了探讨性的研究。
二、 试验
2.1 采用均质材料试件
为了使检测数据具有可比性,应尽可能排除原材料的差异性对试验结果的影响。如图2上海钧测检测技术服务有限公司采用C80灌浆料成型了梯形试件,在尽可能匀质试件的基础上,按设计方案进行各项内容的超声波检测试验。

2.2 试验方案
1)超声对测:
a. 在梯形试件的厚度200mm方向上超声对测;
b. 在梯形试件(踏步)不同尺寸的台阶上超声对测试验,每个台阶上布置3对测点:在100mm、200mm、300mm、400mm方向计12对;翻转梯形试件后,在150mm、250mm、350mm、500mm方向计12对。
2)超声平测:在梯形试件上布置平测法测点,采用“时~距法”得到直线回归方程的截距a。
3)角测法试验:利用上述200mm、250mm、300mm、350mm、400mm等5处超声对测测点的声时平均值进行角测试验。
2.3同声时等效测距法
为了定义超声波角测方法的准确测距,笔者提出了“同声时等效测距法”,即先采用对测法检测到匀质梯形试件不同阶梯测距上的声时值后,再置换能器于超声角测试件丁角两个相邻表面上(利用已知阶梯测距上的对测声时值),且同步移动2个换能器至某一已知对测测距的声时值时停止,根据勾股定理,尝试以已知阶梯测距作为直角三角形的斜边,反推出构件边缘至换能器直径内某点的直角边距A1,测量构件边缘至换能器的近边缘距A2,两数相减得到差值z。即z为超声角测法中真实测距与测量的构件边缘至换能器近边缘距的修正值。

现在的问题是z值如何确定?我们知道超声平测法中求真实测距是采用“时~距法”,取直线回归方程的截距为平测法的修正值a。因为平测法的修正值a是基于2个换能器之间的修正值,在超声角测法中,构件边缘至换能器近边缘距的修正值z仅是对1个换能器的修正值,所以拟考虑套用超声平测法中求真实测距的方法,尝试在试件上先采用“时~距法”平测,取直线回归方程截距a的二分之一作为超声角测法中一条直角边上的修正值z。
2.4检测数据
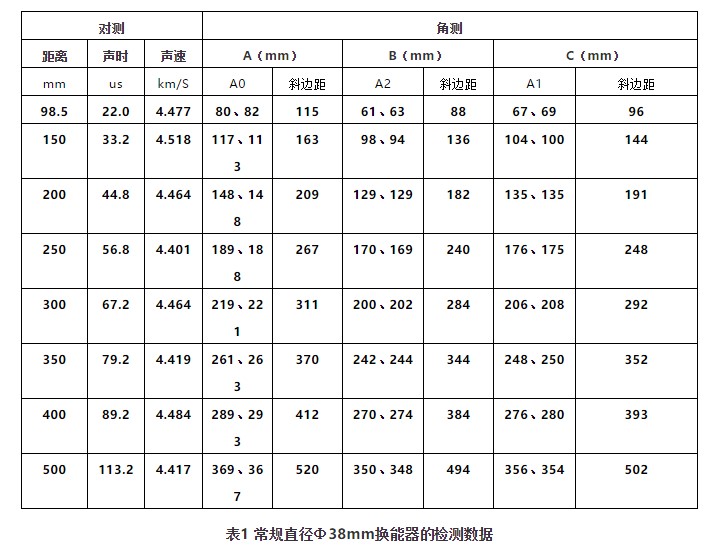
按照“同声时等效测距法”,采用常规换能器直径Ф38mm(频率f=50kHz、零读数t0=12.4 us)在匀质梯形试件不同阶梯测距的检测数据见表1。表1角测中的A、B、C栏分别表示构件边缘至换能器的中心距A0、近边缘距A2、按“同声时等效测距法”修正距A1及其按这2条直角边距计算的斜边距。(超声平测法的直线回归方程L=-12.2+4.379t;z简化取6mm)
三、 检测数据分析
表1所示了8个尺寸不同的踏步面对测的数据以及角测的数据。超声角测采用丁角方法,在试件的2个直角面各置1个换能器。同步移动2个换能器时分别利用(8个尺寸不同的踏步面)对测声时数据,按照“同声时等效测距法”,一边移动一边观察超声仪屏至超声对测时的相同声时时停止,测量构件边缘至换能器的近边缘距A2(虽然同步移动,可能不一定对称,宜测量2个A2距)。根据2个A2距,进行z值修正后计算的角测法斜边测距如C栏所列。
8个尺寸不同的踏步面对测的距离分别是100 mm、150 mm、200 mm、250 mm、300 mm、350 mm、400 mm、500 mm,检测数据表明:
1)频率50kHz、φ=38mm的常规直径换能器无论是采用中心距还是内边距,声时等效距的误差很大,毫无疑问,A栏中心距是正偏差、B栏内边缘距是负偏差;
2)在短测距的时候,在100 mm、150 mm、200 mm、250 mm“角测~对测同声时等效距”的误差比较大,即角测法布置的超声测点A2应该大于250mm;
3)根据试验数据分析,引起“角测~对测同声时等效距”的试验误差,有一些是由对测法时产生的:表1中换能器对测时,相对比较250 mm、300 mm、350 mm、400 mm、500 mm测距,300mm、400mm的声速4.464 km/S、4.484 km/S比250 mm、350 mm、500 mm测距的平均声速4.412 km/S偏大,即67.2 us、89.2 us的检测数值偏小,导致角测时采用的同声时偏小,即使角测~对测同声时等效距偏小。
4)当采用平测法回归系数0.5倍截距修正后,在250 mm、300 mm、350 mm、400 mm、500 mm的误差较小,表明“角测~对测同声时等效距”方法有效。
参考文献:
[1] 童寿兴.混凝土假性碳化引起回弹法强度的误判. 无损检测,2006,8
[2] 谷川恭雄,童寿興,中村正行.超音波法によるコンクリートのひび割れ深さ推定方法に関する研究.日本コンクリート工学協会:コンクリートの非破壊試験法に関するシンポシウム論文集.1991,4













